| Символ (TeX) | Символ (Unicode) | Назва | Значення | Приклад |
|---|---|---|---|---|
| Вимова | ||||
| Розділ математики | ||||
 | ⇒ | Імплікація, слідування |  означає «коли означає «коли  істинне, то істинне, то  також істинне». також істинне».Іноді використовують 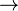 . . |  істинне, але істинне, але 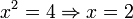 хибно (тому що хибно (тому що  також є розв'язком). також є розв'язком). |
| «з… випливає» або «якщо…, то…» | ||||
| скрізь | ||||
 | ⇔ | Рівносильність |  означає « означає « істинне тоді і тільки тоді, коли істинне тоді і тільки тоді, коли  істинне». істинне». |  |
| «тоді і тільки тоді» або «рівносильно» | ||||
| скрізь | ||||
 | ∧ | Кон’юнкція |  істинне тоді і тільки тоді, коли істинне тоді і тільки тоді, коли  і і  обидва істині. обидва істині. | 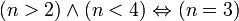 , якщо , якщо  —натуральне число. —натуральне число. |
| «і» | ||||
| Математична логіка | ||||
 | ∨ | Диз’юнкція |  істинне, коли хоча б одна з умов істинне, коли хоча б одна з умов  або або  є істинною. є істинною. | 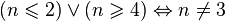 , якщо , якщо  —натуральне число. —натуральне число. |
| «або» | ||||
| Математична логіка | ||||
 | ¬ | Заперечення |  істинне тоді і тільки тоді, коли хибно істинне тоді і тільки тоді, коли хибно  . . | 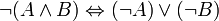  |
| «не» | ||||
| Математична логіка | ||||
 | ∀ | Квантор загальності |  означає « означає «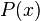 істинне для всіх істинне для всіх  ». ». |  |
| «Для будь-яких», «Для всіх» | ||||
| Математична логіка | ||||
 | ∃ | Квантор існування | 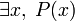 означає «існує хоча б одне означає «існує хоча б одне  таке, що вірно таке, що вірно 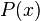 » » |  (підходить число 5) (підходить число 5) |
| «існує» | ||||
| Математична логіка | ||||
 | = | Рівність | 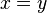 означає « означає « і і  означають один і той же об’єкт». означають один і той же об’єкт». | 1 + 2 = 6 − 3 |
| «дорівнює» | ||||
| скрізь | ||||
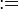 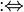  | := :⇔ | Визначення |  означає « означає « за визначенням дорівнює за визначенням дорівнює  ». ». означає « означає « за визначенням рівносильно за визначенням рівносильно  » » |  (Гіперболічний косинус) (Гіперболічний косинус) (Виключаюче або) (Виключаюче або) |
| «дорівнює/рівносильно за визначенням» | ||||
| скрізь | ||||
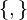 | { , } | Множина елементів |  означає множина, елементами якої є означає множина, елементами якої є  , ,  та та  . . |  (множина натуральних чисел) (множина натуральних чисел) |
| «Множина…» | ||||
| Теорія множин | ||||
 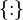 | { | } { : } | Множина елементів, що задовольняють умові |  означає множину усіх означає множину усіх  таких, що істинне таких, що істинне 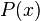 . . |  |
| «Множина всіх… таких, що істинне…» | ||||
| Теорія множин | ||||
  | ∅ {} | Порожня множина |  і і  означає множину, що не містить жодного елементу. означає множину, що не містить жодного елементу. | 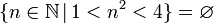 |
| «Порожня множина» | ||||
| Теорія множин | ||||
  | ∈ ∉ | приналежність/неприналежність до множини |  означає « означає « є елементом множини є елементом множини  » » означає « означає « не є елементом не є елементом  » » |   |
| «належить», «з» «не належить» | ||||
| Теорія множин | ||||
  | ⊆ ⊂ | Підмножина |  означає «кожний елемент з означає «кожний елемент з  також є елементом з також є елементом з  ». ».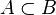 як правило означає те ж, що і як правило означає те ж, що і  . Однак деякі автори використовують . Однак деякі автори використовують  , щоб показати строге включення (а саме , щоб показати строге включення (а саме 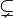 ). ). | 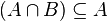  |
| «є підмножиною», «включено в» | ||||
| Теорія множин | ||||
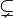 | ⫋ | Власна підмножина |  означає означає  і і 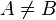 . . | 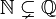 |
| «є власною підмножиною», «строго включається в» | ||||
| Теорія множин | ||||
 | ∪ | Об’єднання |  означає множину елементів, що належать означає множину елементів, що належать  або або  (або обом одразу). (або обом одразу). |  |
| «Об’єднання … і …», «…, об’єднане з …» | ||||
| Теорія множин | ||||
 | ⋂ | Перетин |  означає множину елементів, що належать і означає множину елементів, що належать і  , і , і  . . |  |
| «Перетин … і … », «…, перетнуте з …» | ||||
| Теорія множин | ||||
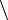 | \ | Різниця множин | 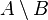 означає множину елементів, що належать означає множину елементів, що належать  , але не належать , але не належать  . . | 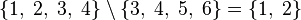 |
| «різниця … і … », «мінус», «… без …» | ||||
| Теорія множин | ||||
 | → | Функція | 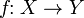 означає функцію означає функцію  , що відображає множину (область визначення) , що відображає множину (область визначення)  у множину у множину  . . | Функція  , що визначення як , що визначення як  |
| «з … в», | ||||
| скрізь | ||||
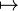 | ↦ | Відображення |  означає, що образом означає, що образом  після застосування функції після застосування функції  буде буде  . . | Функцію, що визначення як  , можна записати так: , можна записати так:  |
| «відображується в» | ||||
| скрізь | ||||
 | N або ℕ | Натуральні числа |  означає множину означає множину 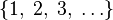 або або 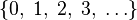 (в залежності від ситуації). (в залежності від ситуації). |  |
| «Ен» | ||||
| Числа | ||||
 | Z або ℤ | Цілі числа |  означає множину означає множину 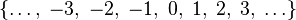 | 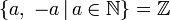 |
| «Зет» | ||||
| Числа | ||||
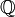 | Q або ℚ | Раціональні числа | 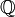 означає означає  |  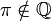 |
| «Ку» | ||||
| Числа | ||||
 | R або ℝ | Реальні числа, або дійсні числа |  означає множину всіх меж послідовностей з означає множину всіх меж послідовностей з 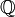 |   ( ( — комплексне число: — комплексне число:  ) ) |
| «Ер» | ||||
| Числа | ||||
 | C або ℂ | Комплексні числа |  означає множину означає множину  |  |
| «Це» | ||||
| Числа | ||||
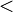  | < > | Порівняння |  означає, що означає, що  є строго меншим від є строго меншим від  . .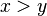 означає, що означає, що  є строго більшим від є строго більшим від  . . |  |
| «менше ніж», «більше ніж» | ||||
| Відношення порядку | ||||
  | ≤ або ⩽ ≥ або ⩾ | Порівняння |  означає, що означає, що  є меншим або дорівнює є меншим або дорівнює  . . означає, що означає, що  є більшим або дорівнює є більшим або дорівнює  . . |  |
| «менше або дорівнює»; «більше або дорівнює» | ||||
| Відношення порядку | ||||
 | ≈ | Приблизна рівність |  з точністю до з точністю до 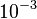 означає, що 2,718 відрізняється від означає, що 2,718 відрізняється від  не більше ніж на не більше ніж на 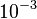 . . |  з точністю до з точністю до 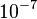 . . |
| «приблизно дорівнює» | ||||
| Числа | ||||
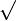 | √ | Арифметичний квадратний корінь | 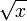 означає додатне дійсне число, яке в квадраті дає означає додатне дійсне число, яке в квадраті дає  . . |   |
| «Корінь квадратний з …» | ||||
| Числа | ||||
 | ∞ | Нескінченність |  та та  суть елементи розширеної множини дійсних чисел. Ці символи позначають числа, що є меншими/більшими від усіх дійсних чисел. суть елементи розширеної множини дійсних чисел. Ці символи позначають числа, що є меншими/більшими від усіх дійсних чисел. |  |
| «Плюс/мінус нескінченність» | ||||
| Числа | ||||
 | | | | Модуль числа (абсолютне значення), модуль комплексного числа або потужність множини |  означає абсолютну величину означає абсолютну величину  . . означає потужність множини означає потужність множини  та дорівнює, якщо та дорівнює, якщо  скінченна, числу елементів скінченна, числу елементів  . . |  |
| «Модуль»; «Потужність» | ||||
| Числа и Теорія множин | ||||
 | ∑ | Сума, сума ряду | 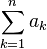 означає «сума означає «сума  , де , де  приймає значення від 1 до приймає значення від 1 до », а саме », а саме 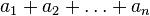 . . означає суму ряду, що складається з означає суму ряду, що складається з  . . | 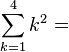  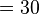 |
| «Сума … по … від … до …» | ||||
| Арифметика, Математичний аналіз | ||||
 | ∏ | Добуток | 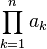 означає «добуток означає «добуток  для усіх для усіх  від 1 до від 1 до  », а саме », а саме |   |
| «Добуток … по … від … до …» | ||||
| Арифметика | ||||
 | ∫ | Інтеграл |  означає «Інтеграл від означає «Інтеграл від  до до  функції функції  від від  по змінній по змінній  ». ». |   |
| «Інтеграл (від … до …) функції … по…» | ||||
| Математичний аналіз | ||||
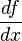 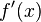 | df/dx f'(x) | Похідна | 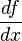 або або 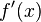 означає «(перша) похідна функції означає «(перша) похідна функції  від від  по змінній по змінній  ». ». |  |
| «Похідна … по …» | ||||
| Математичний аналіз | ||||
  |   | Похідна  -го порядку -го порядку |  або або  (в другому випадку якщо (в другому випадку якщо  — фіксоване число, то воно пишеться римськими цифрами) означає « — фіксоване число, то воно пишеться римськими цифрами) означає « -я похідна функції -я похідна функції  від від  по змінній по змінній  ». ». |  |
"Мова математиків"
Підписатися на:
Коментарі (Atom)
Немає коментарів:
Дописати коментар